くり下がりのある引き算の練習ステップ

くり下がりのある引き算攻略法まとめ

【最初にお断り】

このページは低学年の難所「くり下がり」踏むべき練習段階を整理したものですが、簡単に整理しただけですので今のところ学校教員・塾講師など、教育関係者以外の方が見られても、あまりお役には立たないかもしれません。

保護者の皆さんが使用される場合はこの点注意して下記の「実際に使用したやり方は...」をご参照の上、無理しないようにご利用下さい。尚、利用に関しては個人差もありますので結果の責任は負いかねますのでご了承下さい。

---

このページを制作した理由、実を言うと何のことはない、うちの息子、小２である程度できていたはずの「くり下がり」が小３後半の割り算が始まる頃になって相当怪しくなっていたのである。

どーせある程度困ってからでないとなかなかやらないし、どうせ教え方は決まっているし、まあいいやとばかりに思ってしばらく放っておいたのが原因であるのである。

いやあ、分かっていて放っておくとは実にひどい親である。

で、責任をもって？・・・三日ほど、くり下がりの復習をして事なきを得たが、ついでだったので、拙熊が教えるときに踏む段階をまとめてみた

塾や家庭教師のときに使っていた手口そのまんまで、実際大して時間も食わないが、その割に意外に多段階を踏んでいるに自分でも驚いてしまった。時間をかけないで効率よくやるためのセット教材ができてしまったがこちらはまだ電子化していない・・・・要望があればことによると電子化するか・・・・

実際使用したやり方はというと下記のような感じ。

各段階をそれぞれ１枚６問～８問程度のプリント学習教材とし、数枚を１クールとして問題をやらせる。次の段階にをクリアしたところで、前の段階のものとの混合問題を与える。

混合問題がクリアできたらさらに次のステップへ進む　まあ、こんなところだ。すすみ具合にもよるが、５０～１００枚ほどの量になるだろう。但し一枚の分量が少ないのでさしたる抵抗はないだろう。その年代の子どもにとっては「クリアした枚数が多いこと」がけっこう励みになるようでもあるので、一枚の問題数を増やさない方が良いようだ。

大きめの方眼系の用紙を使うか、エクセルでセルの枠ごと印刷する等で、桁がきちんと認識できるようにするほうが手っ取り早い。

---

１）ｎ桁－１桁

（Ａ）末尾が０の数から１桁の数を引く

（１）２桁で末尾０の数から１桁の数を引く

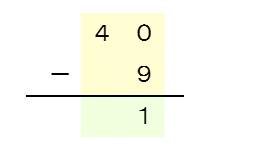
（２）ｎ桁で先頭桁が１で先頭桁以外が０の数から１桁の数を引く

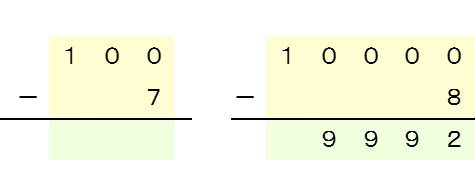
（３）ｎ桁で先頭桁以外が０の数から１桁の数を引く

（４）ｎ桁（４桁以上）で下から３桁目が１、かつ、下２桁が０の数から１桁の数を引く

（５）ｎ桁（４桁以上）で下から３桁目が１以外、下２桁が０の数から１桁の数を引く

（６）ｎ桁（４桁以上）で、下２桁が０の数から１桁の数を引く　（４）（５）混合

(Ｂ)末尾が０以外の数から１桁の数を引く

（１）末尾が０以外で、２桁の数から１桁の数を引く

（２）末尾が０以外で、２桁の数から２桁の数を引く

（３－１）末尾が０以外で、ｎ桁で下から２桁目の数が１の数から１桁の数を引く

（３－２）末尾が０以外で、ｎ桁で下から２桁目の数が１でない数から１桁の数を引く

（４）末尾が０以外で、ｎ桁の数から１桁の数を引く　（（３－１），（３－２）の混合）

２）特殊な３桁－２桁

（１）下から２桁目が０の３桁の数から２桁の数を引く　（くり下がり２回）

くり下がりの連続に慣れ、前の桁の数字によらず、適切な方法でくり下がりをできるようにする。

（２）下から２桁目が０の３桁の数から２桁の数を引く　（くり下がり１回：下から２桁目）

はじめくり下がり無しの計算から入り、次の桁でくり下がりが生じる場合の間違い防止
（くり下がりありの部分と無しの部分の混合を体験させる）

３）ｎ桁－２桁

（１）くり下がりの結果、９になった桁からさらに引くパターン（再くり下がりは生じない）

（２）くり下がりの結果、０になった桁からさらに引くパターン

１．下から３桁目が０以外の場合（再くり下がりは必ず生じる）

（Ｐ、ｘ、ｙ、ｚ、ｎ、ｍは任意の数字、但しP以外は下の条件に合致するもの）

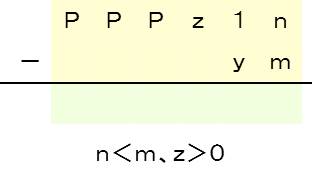
２．下から３桁目が０の場合（３桁目を９にしなければならないケース、再くり下がりは必ず生じる）

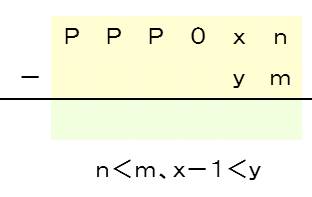
３．下から３桁目が０の場合（３桁目を９にしなければならなく、かつ、下から２桁めが０になるケース
：再くり下がりは必ず生じる）

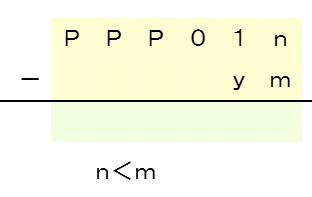
（３）くり下がりの結果、１～８になった桁からさらに引くパターン（再くり下がり無し）

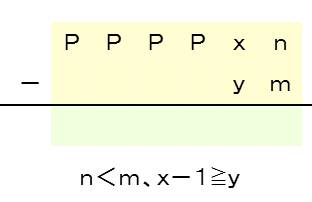
（４）くり下がりの結果、１～８になった桁からさらに引くパターン（再くり下がり有り）

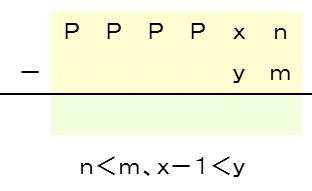
（５）（１）～（４）混合

４）ｎ桁－ｍ桁混合

とまあ、ここまででステップは終了。

ここまでステップを踏んで練習すればそう簡単に崩れないようになるだろう。

---

結論から言ってしまうと、２００２年指導要領で小学校２年生でのくり下がりの計算が３桁までに制限されてしまうのは、かなりまずいことだと考えられる。なぜなら子供は「メカニズム」を追うだけで計算ができるようになる訳じゃ胃からだ。

上記でＰという文字で表された任意の数、その桁数が「一つ、二つ、三つ・・ことによると四つ」とまあ、ある程度のパターンを通り抜けて「二度あることは３度ある」という感覚をつかむまでは、「メカニズム」をうまく運用できないというのが子供というものだ。

この段階での落ちこぼれは理解が足りないんじゃない。「メカニズム連動の運用練習」が足りないんだ。

ツイート

投稿者：狸穴猫

身近な自由研究ネタ（２）　社会編＜ ＴＯＰ ＞タコを追え１　追従視のトレーニング

▲このページのトップに戻る
▲なぜか学習指導へ戻る

狸穴通信 INDEX